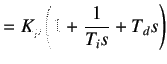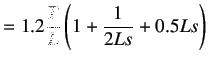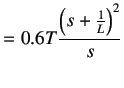Figure 5.2:
Reaction curve [1]
|
 |
Ziegler-Nichols rule determines the values of gain 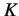 , integral time
, integral time  and derivative time
and derivative time 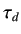 based on
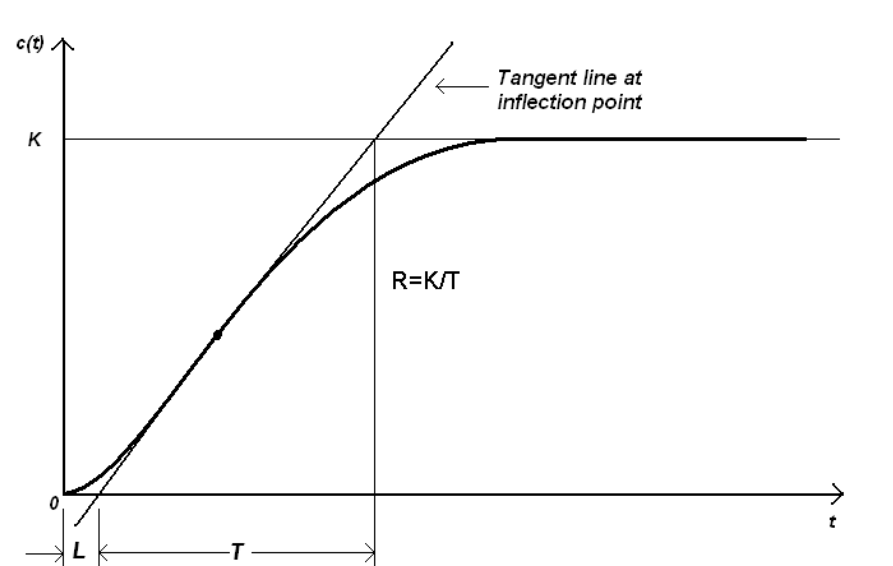
the step response characteristics of a given plant. In this method, one can experimentally obtain the response of a plant
to a step input, as shown in figure 5.2. This method is applicable only when the response to the step input exhibits
S-shaped curve [3].
based on
the step response characteristics of a given plant. In this method, one can experimentally obtain the response of a plant
to a step input, as shown in figure 5.2. This method is applicable only when the response to the step input exhibits
S-shaped curve [3].
As shown in figure 5.2, by drawing the tangent line at the inflection point and determining the intersection of the
tangent line with the time axis and the line  ,we get two constants, namely, delay time
,we get two constants, namely, delay time 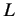 and time constant
and time constant 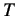 .
.
Ziegler and Nichols suggested to set the values of
 according to the formula shown in table 5.1.
according to the formula shown in table 5.1.
Table 5.1:
Ziegler-Nichols tuning rule based on step response of plant
|
|
Notice that the PID controller tuned by the Ziegler-Nichols rule gives,
Thus, the PID controller has a pole at the origin and double zeros at 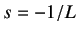 .
.
rokade
2017-04-23
![]() according to the formula shown in table 5.1.
according to the formula shown in table 5.1.