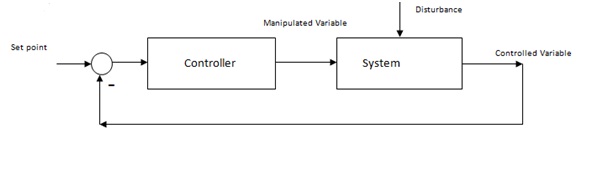
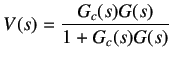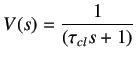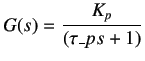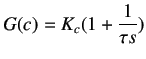Figure 9.1:
Closed loop circuit
|
 |
We have
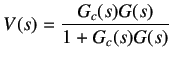 |
(9.2) |
where
V(s) : Overall closed-loop transfer function
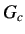 (s) : Controller transfer function
(s) : Controller transfer function
G(s) : System transfer function.
Therefore,
 |
(9.3) |
Let the desired closed loop transfer function be of the form
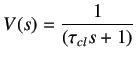 |
(9.4) |
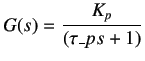 |
(9.5) |
By using the equations for G(s) and V(s), we get
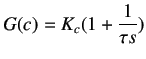 |
(9.6) |
where,
 |
(9.7) |
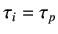 |
(9.8) |
When 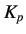 and
and 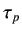 are known as a function of time, the values of
are known as a function of time, the values of 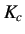 and
and  can be found as functions of
temperature as well.
rokade
2017-04-23
can be found as functions of
temperature as well.
rokade
2017-04-23