Next: Implementing locally Up: Controlling Single Board Heater Previous: Implementing virtually
The PID controller in continuous time is given by
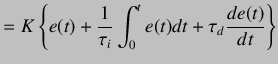 |
(5.37) | |
|
On taking the Laplace transform, we obtain
| ||
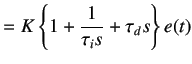 |
(5.38) | |
|
By mapping controller given in equation 5.38 to the discrete time domain using backward difference formula, we get
| ||
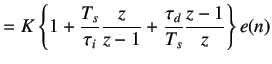 |
(5.39) | |
|
On cross multiplying, we obtain
| ||
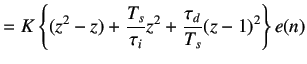 |
(5.40) | |
|
We divide by
| ||
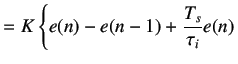 |
||
![$\displaystyle + \left. \frac{\tau_d}{T_s}[e(n)-2e(n-1)+e(n-2)]\right\}$](img197.png) |
(5.41) | |
|
The PID controller is usually written as
| ||
| (5.42) | ||
|
where
| ||
![$\displaystyle =K\left[1+\frac{T_s}{\tau_i}+\frac{\tau_d}{T_s}\right]$](img199.png) |
(5.43) | |
![$\displaystyle =K\left[-1-2\frac{\tau_d}{T_s}\right]$](img200.png) |
(5.44) | |
![$\displaystyle =K\left[\frac{\tau_d}{T_s}\right]$](img202.png) |
(5.45) | |