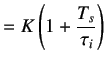PI Controller

Figure 9.11: Xcos diagram for PI controller

The PI Controller in continuous time is given by

$$u(t) = K \left[e(t) + \frac 1{\tau_i}\int_0^t e(t)dt\right]$$ (9.9)

On taking Laplace transform, we obtain

$$u(s) = K \left[1 + \frac 1{\tau_i s}\right]e(s)$$ (9.10)

By mapping equation 9.10 to discrete time interval using Backward Difference Approximation, we get

$$u(n) = K \left[1 + \frac{T_s}{\tau_i} \frac{z}{z-1}\right]e(n)$$ (9.11)

On cross multiplication, we obtain

$$(z-1)\times u(n) = K \left[(z-1) + \frac{T_s}{\tau_i} (z)\right]e(n)$$ (9.12)

We divide by z, and using the shifting theorem, we obtain

$$u(n) - u(n-1) = K \left[e(n) - e(n-1) + \frac{T_s}{\tau_i} e(n)\right]$$ (9.13)

The PI Controller is usually written as

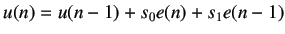$$u(n) = u(n-1) + s_0 e(n) + s_1 e(n-1)$$ (9.14)

where,

$$s_0 =K\left(1+\frac{T_s}{\tau_i}\right)$$

$$s_1 =-K$$