2-DOF Controller Design using the Pole Placement Method [1]

2-DOF Controller Design using the Pole Placement Method [1]

A 2-DOF pole placement controller is shown in figure 6.3. We will not consider the effect of external disturbance in the design. The controller will be designed for setpoint tracking.

**Figure 6.3:** 2-DOF pole placement controller

We want the desired output, , of the system to be related to the setpoint in the following manner:

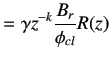$\displaystyle Y_m(z)$	$\displaystyle =\gamma z^{-k}\frac{B_r}{\phi_{cl}}R(z)$	(6.14)
$\phi_{cl}$ is the desired closed loop characteristic polynomial obtained from the desired region analysis. Please refer to [1] for more information on desired region analysis. $\gamma$ is chosen such that equals the setpoint at steady-state. Therefore $\gamma$ is given by,
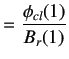$\displaystyle \gamma$	$\displaystyle =\dfrac{\phi_{cl}(1)}{B_r(1)}$	(6.15)
Simplifying the block diagram shown in figure 6.3 yields
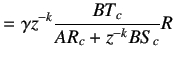$\displaystyle Y$	$\displaystyle =\gamma z^{-k}\frac{BT_c}{AR_c+z^{-k}BS_c}R$	(6.16)
We have dropped the argument of for convenience. We want the output of the system to be equal to the desired output . Equating equations 6.14 and 6.16 we get
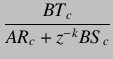$\displaystyle \frac{BT_c}{AR_c+z^{-k}BS_c}$	$\displaystyle =\frac{B_r}{\phi_{cl}}$	(6.17)
We can expect some cancelations between the numerator and the denominator polynomials in the LHS, thereby making . But the cancelations, if any, must be between poles and zeros. One should avoid the cancelation of an unstable pole with an unstable zero. Let us split the factors of the numerator and denominator polynomials, and , of the plant into and factors. Therefore, we write and as
$\displaystyle A$	$\displaystyle =A^gA^b, B=B^gB^b$	(6.18)

We also define

and

as

$\displaystyle R_c$	$\displaystyle =B^gR_1$	(6.19)
$\displaystyle S_c$	$\displaystyle =A^gS_1$	(6.20)
$\displaystyle T_c$	$\displaystyle =A^gT_1$	(6.21)

Hence, equation 6.17 becomes

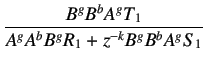$\displaystyle \frac{B^gB^bA^gT_1}{A^gA^bB^gR_1+z^{-k}B^gB^bA^gS_1}$	$\displaystyle =\frac{B_r}{\phi_{cl}}$	(6.22)
After cancelling out the common factors, we obtain
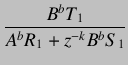$\displaystyle \frac{B^bT_1}{A^bR_1+z^{-k}B^bS_1}$	$\displaystyle =\frac{B_r}{\phi_{cl}}$	(6.23)
We obtain,
$\displaystyle B^bT_1$	$\displaystyle =B_r$	(6.24)
$\displaystyle A^bR_1+z^{-k}B^bS_1$	$\displaystyle =\phi_{cl}$	(6.25)
Equation 6.26 is known as the Aryabhatta's identity and can be used to solve for and . One can choose in many ways. If we choose the 2-DOF controller is reduced to a 1-DOF controller. Let us choose . Therefore equation 6.25 becomes
$\displaystyle B^b$	$\displaystyle =B_r$	(6.26)
The expression for $\gamma$ now becomes
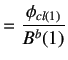$\displaystyle \gamma$	$\displaystyle =\frac{\phi_{cl(1)}}{B^b(1)}$	(6.27)
and the desired closed loop transfer function will be
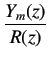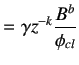$\displaystyle \frac{Y_m(z)}{R(z)}$	$\displaystyle =\gamma z^{-k}\frac{B^b}{\phi_{cl}}$	(6.28)

One can see that the open loop plant model imposes two limitations on the closed loop transfer function.

The bad portion of the open loop model cannot be canceled out and it appears in the closed loop model.
The open loop plant delay cannot be removed or minimized, i.e., the closed loop model cannot be made faster than the open loop model.

rokade 2017-04-23