Next: Procedure to calculate 2DOF Up: 2-DOF Controller theory and Previous: 2-DOF Controller Design using
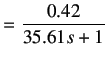 |
(6.29) | |
|
with a time constant of
| ||
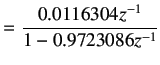 |
(6.30) | |
|
Let us now define the transient specifications. We choose Rise Time =100 s and Overshoot (
| ||
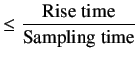 |
||
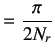 |
||
|
and
| ||
|
The closed loop characteristic polynomial is given by,
| ||
|
Refer to the Scilab code desired.sci to calculate
| ||
|
Recall that we have not considered external disturbance in the block diagram shown in figure 6.3. However, we can still up to some extent take care of the disturbances. This is achieved by using the Internal Model Principle. If a model of step is present inside the loop, step disturbances can be rejected [1]. We can apply this by forcing
| ||
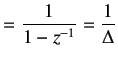 |
||
|
Therefore,
| ||
|
| ||
All the above calculations are incorporated into a single Scilab code named twodof_para.sce 6.2.