2-DOF Controller theory and Calculations

Controllers are broadly divided into two categories: feedback and feed forward controllers. Feed forward controllers are those that take control action before a disturbance affects the plant. But this requires an ability to sense the disturbance accurately. Moreover, exact knowledge of the plant is also needed. As a result, a feed forward control strategy is rarely used alone.

A feedback control strategy is shown in figure 6.1. The reference and the output are continuously compared to generate error , which is fed to the controller , to take appropriate control action. is the controller output that is fed to the plant. Unlike feed forward controllers, exact knowledge of the plant and the disturbance is not necessary in this case. Feedback controllers are further classified as One Degree of Freedom (1-DOF) controllers and Two Degrees of Freedom (2-DOF) controllers. Degree of freedom refers to the number of parameters that are free to vary in a system. A higher degree of freedom controller makes the plant less susceptible to disturbances.

**Figure 6.1:** Feed back control strategy

The expression for output, of the system shown in figure 6.1 is given by

$\displaystyle Y(z)$

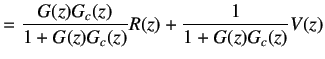$\displaystyle =\frac{G(z)G_c(z)}{1+G(z)G_c(z)}R(z)+\frac 1{1+G(z)G_c(z)}V(z)$

(6.1)

This expression can be written in mixed notation [1] as

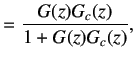$\displaystyle y(n)$	$\displaystyle =\frac{G(z)G_c(z)}{1+G(z)G_c(z)}r(n)+\frac 1{1+G(z)G_c(z)}v(n)$	(6.2)
Let,
$\displaystyle T(z)$	$\displaystyle =\frac{G(z)G_c(z)}{1+G(z)G_c(z)} , \,$	(6.3)
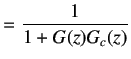$\displaystyle S(z)$	$\displaystyle =\frac 1{1+G(z)G_c(z)}$	(6.4)
Therefore,
$\displaystyle y(n)$	$\displaystyle =T(z)r(n)+S(z)v(n)$	(6.5)

The controller has to track the reference input as well as eliminate the effect of external disturbance. So ideally, we want T = 1 and S = 0. But, it is not possible to achieve both the requirements simultaneously using this control strategy. This control strategy is called One Degree of Freedom, abbreviated as 1-DOF.

A Two Degrees of Freedom controller is as shown in figure 6.2. Here, and together constitute the controller. is in the feedback path and is used to eliminate the effect of disturbances, whereas is in the feed forward path and is used to help the output track the reference input.

**Figure 6.2:** 2DOF feed back control strategy

The expression for control effort in figure 6.2 is given by

$\displaystyle u(n)$	$\displaystyle = r(n)G_f - y(n)G_b$	(6.6)
Let
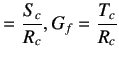$\displaystyle G_b$	$\displaystyle = \frac{S_c}{R_c} , G_f = \frac{T_c}{R_c}$	(6.7)
where , and are polynomials in $z^{-1}$ .We get
$\displaystyle R_c(z)u(n)$	$\displaystyle =T_c(z)r(n)-S_c(z)y(n)$	(6.8)
Consider a plant whose model is given by
$\displaystyle A(z)y(n)$	$\displaystyle =z^{-k}B(z)u(n)+v(n)$	(6.9)
Substituting equation 6.8 in equation 6.9, we get
$\displaystyle Ay(n)$	$\displaystyle =z^{-k}\frac{B}{R_c}\bigg[T_cr(n)-S_cy(n)\bigg]+v(n)$	(6.10)
Solving for ,
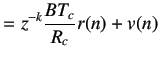$\displaystyle \bigg(\frac{R_cA+z^{-k}BS_c}{R_c}\bigg)y(n)$	$\displaystyle =z^{-k}\frac{BT_c}{R_c}r(n)+v(n)$	(6.11)
This can also be written as
$\displaystyle y(n)$	$\displaystyle =z^{-k}\frac{BT_c}{\phi _{cl}}r(n)+\frac{R_c}{\phi _{cl}}v(n)$	(6.12)
where $\phi_{cl}$ is the closed loop characteristic polynomial given by
$\displaystyle \phi _{cl}$	$\displaystyle =R_c(z)A(z)+z^{-k}B(z)S_c(z)$	(6.13)

We want the following conditions to be satisfied while designing a controller.

The zeros of $\phi_{cl}$ should be inside the unit circle, so that the closed-loop system becomes stable
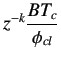The value of $z^{-k}\dfrac{BT_c}{\phi _{cl}}$ must be close to unity, so that reference tracking is achieved
The value of $\dfrac{R_c}{\phi _{cl}}$ must be as small as possible to achieve disturbance rejection

We shall now see the pole placement controller approach to design a 2-DOF controller.

Subsections

rokade 2017-04-23